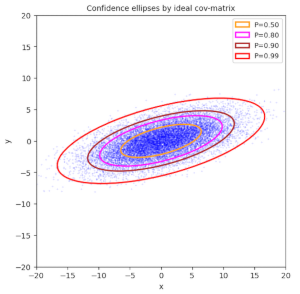
How to compute confidence ellipses – I – simple method based on the Pearson correlation coefficient
This post was motivated by a publication of Carsten Schelp [1]. Actually, a long time ago. I used his results in 2021, when I had to plot confidence ellipses during the analysis of statistical (multivariate) vector distributions produced a Machine Learning algorithm. So, all acknowledgements belong to Schelp’s work. However, his ideas have also triggered some of my own efforts… Read More »How to compute confidence ellipses – I – simple method based on the Pearson correlation coefficient