Skip to content

ResNets

Posts on Residual Networks

ResNet56V2 Convergence within epoch 20

AdamW for a ResNet56v2 – VI – Super-Convergence after improving the ResNetV2

In previous posts of this series I have shown that a Resnet56V2 with AdamW can converge to acceptable values of the validation accuracy for the CIFAR10 dataset – within less than 26 epochs. An optimal schedule of the learning rate [LR] and optimal values for the weight decay parameter [WD] were required. My network – a variation of the ResNetV2-structure… Read More »AdamW for a ResNet56v2 – VI – Super-Convergence after improving the ResNetV2

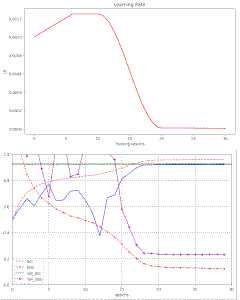
Short ResNet training on CIFAR10 over 21 epochs

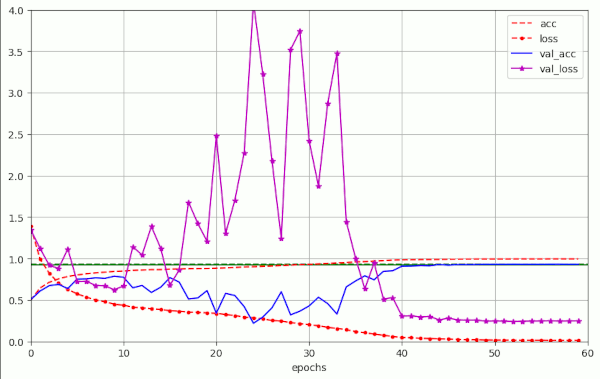
AdamW for a ResNet56v2 – V – weight decay and cosine shaped schedule of the learning rate

In this post series we try to find methods to reduce the number of epochs for the training of ResNets on image datasets. Our test case is CIFAR10. In this post we will test a modified cosine shaped schedule for a systematic and fast reduction of the learning rate LR. This supplements the approaches described in previous posts of this… Read More »AdamW for a ResNet56v2 – V – weight decay and cosine shaped schedule of the learning rate

AdamW for a ResNet56v2 – IV – better accuracy and shorter training by pure weight decay and large scale fluctuations of the validation loss

Among other thins this post series is about efforts to reduce the number of training epochs for ResNets. We test our ideas with a ResNet applied to CIFAR10. So far we have tried out rather simple methods as modifying the schedule for the learning rate [LR]. In this post I describe experiments regarding a model using the AdamW optimizer, without… Read More »AdamW for a ResNet56v2 – IV – better accuracy and shorter training by pure weight decay and large scale fluctuations of the validation loss

AdamW for a ResNet56v2 – III – excursion: weight decay vs. L2 regularization in Adam and AdamW

A major topic of this post series is the investigation of methods to reduce the number of required training epochs for ResNets. In particular with respect to image analysis. Our test case is defined by a ResNet56v2 neural network trained on the CIFAR10 dataset. For intermediate results of numerical experiments see the first two posts During the last week I… Read More »AdamW for a ResNet56v2 – III – excursion: weight decay vs. L2 regularization in Adam and AdamW