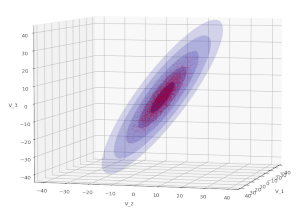
Bivariate Normal Distribution – Mahalanobis distance and contour ellipses
I continue with my posts on Bivariate Normal Distributions [BVDs]. In this post we consider the exponent of a BVD’s probability density function [pdf]. This function is governed by a central matrix Σ-1, the inverse of the variance-covariance matrix of the BVD’s random vector. We define the so called Mahalanobis distance dm for BVD vectors. A constant value of the… Read More »Bivariate Normal Distribution – Mahalanobis distance and contour ellipses