Iterative method to compute the covariance-matrix of normal MVN-like inner cores of multivariate distributions with strongly asymmetric outer layers – I
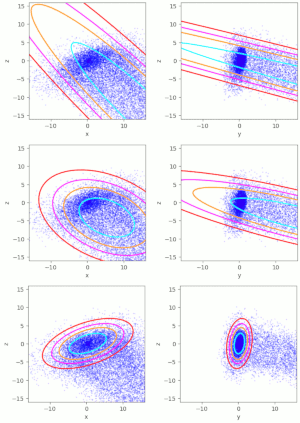
In other posts in this blog (see [1] to [3]), I have discussed multiple methods to calculate and construct confidence ellipses of “Bivariate Normal Distributions” [BVNs]. BVNs are the marginal distributions of “Multivariate Normal Distributions” [MVNs] in e.g. n dimensions ( n > 2). Therefore, two-dimensional confidence ellipses appear as projections of n-dimensional concentric confidence ellipsoids of MVNs onto (2-dim) coordinate planes. The properties of the confidence ellipsoids, which also give us contours of the probability density, are defined by the variance-covariance matrix Σ of the MVN. This post discusses a method to compute the confidence ellipsoids and ellipses for an inner MVN-like core of an otherwise largely asymmetric distribution, which in its overall shape and structure deviates strongly from a MVN.
Read More »Iterative method to compute the covariance-matrix of normal MVN-like inner cores of multivariate distributions with strongly asymmetric outer layers – I