Properties of BVD confidence ellipses – II – dependency of the half-axes on the correlation coefficient
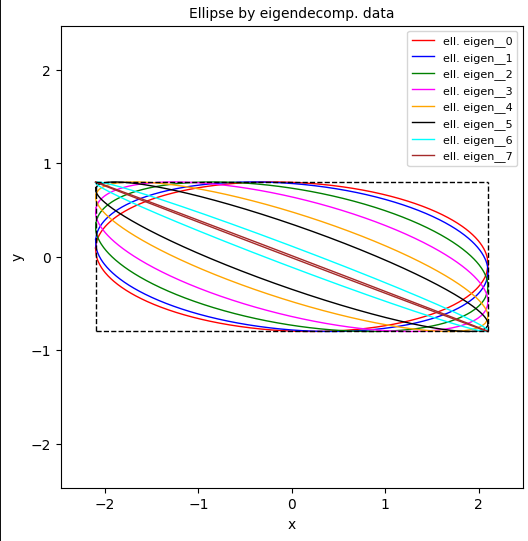
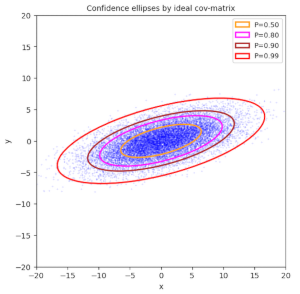
If you have read my last post on confidence ellipses, you may have tried to derive the result on the longer half-axis for maximum correlation by following an eigenvalue analysis of the (inverse) covariance matrix of a Bivariate Normal Distribution [BVD]. If you have succeeded, jump over this post. If not, the contents my be interesting for you. Its is… Read More »Properties of BVD confidence ellipses – II – dependency of the half-axes on the correlation coefficient