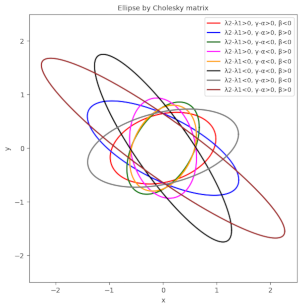
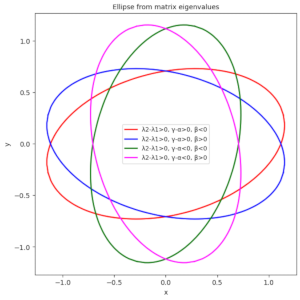
Ellipses via matrix elements – II – numerical tests of formulas
During the last posts, I have discussed properties of ellipses and ways to (re-) construct them from elements of a symmetric, invertible and positive-definite (2×2)-matrix, which defines a quadratic form. In the context of Machine Learning we often have to determine confidence ellipses from elements of a numerically determined variance-covariance matrix of statistical bivariate vector-distributions. Formulas relating the geometric properties… Read More »Ellipses via matrix elements – II – numerical tests of formulas