Skip to content

Machine Learning

ResNet56V2 Convergence within epoch 20

AdamW for a ResNet56v2 – VI – Super-Convergence after improving the ResNetV2

In previous posts of this series I have shown that a Resnet56V2 with AdamW can converge to acceptable values of the validation accuracy for the CIFAR10 dataset – within less than 26 epochs. An optimal schedule of the learning rate [LR] and optimal values for the weight decay parameter [WD] were required. My network – a variation of the ResNetV2-structure… Read More »AdamW for a ResNet56v2 – VI – Super-Convergence after improving the ResNetV2

CAE generated face on background of a MND

Latent space distribution of a CAE for face images – I – unenforced Multivariate Normal Distributions

The analysis of face images by a trained Autoencoder and the generation of face images from statistical vectors is a classical task in Machine Learning. In this post series I want to clarify the properties of vector distributions for face images generated by a trained standard Convolutional Autoencoder [CAE] in its latent space. The dataset primarily used is the CelebA… Read More »Latent space distribution of a CAE for face images – I – unenforced Multivariate Normal Distributions

Concentric surfaces of ellipsoids

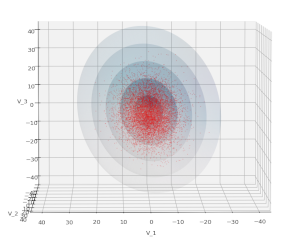
Multivariate Normal Distributions – III – Variance-Covariance Matrix and a distance measure for vectors of non-degenerate distributions

In previous posts of this series I have motivated the functional form of the probability density of a so called “non-degenerate Multivariate Normal Distribution“. In this post we will have a closer look at the matrix Σ that controls the probability density function [pdf] of such a distribution. We will show that it actually is the covariance matrix of the… Read More »Multivariate Normal Distributions – III – Variance-Covariance Matrix and a distance measure for vectors of non-degenerate distributions

contour ellipsoids of a projected MND

Multivariate Normal Distributions – I – Basics and a random vector of independent Gaussians

This post series is about mathematical aspects of so called “Multivariate Normal Distributions“. In the literature two abbreviations are common: MNDs or MVNs. I will use both synonymously. To get an easy access I want to introduce MNDs as the result of a linear transformations applied to random vectors whose components can be described by independent 1-dimensional normal distributions. Afterward… Read More »Multivariate Normal Distributions – I – Basics and a random vector of independent Gaussians