When you start working with Artificial Neural Networks [ANNs] there are a lot of things you must get familiar with: Different types of networks and network layers, weights, signal propagation, loss, backward error propagation, gradient descent, regularization, normalization, tensors (arrays) …. In addition you may have to fight with complex layer structures even for relatively simple experiments. And the objects you work with will typically be described in high-dimensional variable spaces.
The good news is that one can study most of these subjects already with an extremely simple artificial network consisting of only a few neurons:
- two or more stupid neurons to receive and transfer input data
- one central computing neuron, which picks up the input data, processes them and produces some output
- a bias neuron.
Depending on properties of the central such a simple ANN-configuration is called a “Perceptron”, an “Adaline” or a “logistic classifier”. They have in common that a single computing neuron can only be trained to solve a very limited class of problems. But its math is easy to understand. Especially, when we work with objects that can be described by very few variables. And: Although being rather simple our network can be equipped with properties that classify it as a primitive example of a real ANN.
This blog-series uses a single neuron and very simple input objects to study some central aspects and terms of ANN-related Machine Learning techniques. We will train our compute neuron to solve a classification task. We will define a set of simple example data which shall be used as the basis of a training process. These data quantify the “objects” which the algorithm shall use to establish criteria for a later classification of yet unknown, but structurally equal data samples.
In contrast to more complex ML-experiments we will deal with objects that can be described by two variables, only. The math controlling our primitive network can be followed analytically and with directly interpretable 2D- and 3D-plots. We will define required functions such that they enable us to discuss the gradient descent method and related problems thoroughly. We will also briefly discuss the mathematical reasons for the severe limitations of a single neuron’s capabilities, in particular when used in the form of a perceptron.
One important lessons will be that we sometimes have to transform the input data in an appropriate way to get optimal results. This means in general that the mathematical variables to describe the objects of a ML-problem must be chosen carefully. The choice has to match both the object properties and the functional abilities of an ANN’s architecture.
Level of the post series: Beginners with some mathematical background
You need to know what exponential functions are and how the derivatives of such functions are calculated. Furthermore you need to know how one can determine the extrema of a 1- or 2-dimensional function. If you are not familiar with 2-dimensional calculus you will have to accept some definitions. But you will hopefully understand most of the contents by studying instructive data plots. You should, however, know how one defines points in a 2-dimensional coordinate system by a tuple of coordinate values. You should also know or accept what position vectors are. I will indicate the relation of the neuron’s operations to matrix multiplications (linear algebra). All in all the level in math is something between the 1st and 2nd semester at university. But I think also pupils at high-school do have a chance.
Regarding programming aspects: We will use simple Python code on a CPU. You need to be familiar with Numpy and real value arrays. A GPU, Tensorflow and Keras are not required.
A simple neural network for a single computing neuron
In a first approach I omit the bias neuron, reduce the number of input neurons to 2 and set the number of the central neuron’s output channels to just one. I.e. the compute neuron produces only one number for any set (= tuple) of input data.
All in all we deal with 3 neurons. But only one of these neurons is “intelligent” in the sense that it performs some computing. I therefore call it the “compute neuron” [CN]. I have depicted the network below.
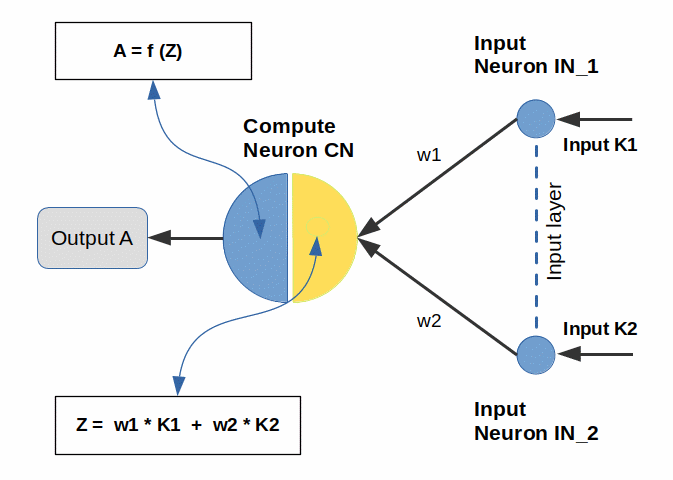
We see two input neurons, IN_1 and IN_2. Each input neuron receives input via an input data channel. The input channels are labeled as by K1 and K2. You can regard the input arriving at a particular input neuron as a pulse-like signal whose amplitude is measured in some appropriate units.
Note: In standard ANNs a continuous signal shape, i.e. a varying amplitude vs. time, is not of interest. We focus on the signal strength (amplitude), only, at certain discrete processing steps of the network.
A general ANN-neuron may receive a signal and modify its strength. It transfers the resulting output signal via available connections to other neurons or output devices. Even in our simple network the three depicted neurons are connected: The input signals are transferred from the input neurons to the central neuron [CN]. The “compute neuron” CN works with the input and generates some output signal. The output is provided along an output-channel A, where it can be read and interpreted by some interested external devices or receivers.
Our neurons IN_1 and IN_2 just transfer the signals without modifying them. They were basically introduced to get well defined addresses for our input data. They are just signal gateways. We could even have omitted them.
Remark: In many ML-textbooks the input neurons of a perceptron or an Adaline are omitted assuming that we just control input data channels to a single (computing) neuron. I have, however, added input neurons from the beginning as most ML-frameworks for programming ANNs actually do define an input layer of input neurons.
Our single “compute neuron” CN has an active input side (yellow) and an active output side (blue). The input side applies a linear transformation to the incoming signals. This operation results in an intermediate signal “Z“. The output side of CN modifies Z by applying a function f(Z): Z is inserted as an argument. This step delivers an output signal A = f(Z). The neuron’s output can in our example be registered and evaluated by some external appliance. In more complex networks the output of a specific neuron would instead be delivered to further neurons (of other network layers).
The function f(Z) of ANN-neurons is in general assumed to be continuous, to contain some non-linear terms and to be at least piece-wise differentiable. It is called “activation function“.
In complex ANNs with many layers (each containing many compute neurons) the type of activation function may not be the same for all neurons. It may differ from layer to layer or may vary between particular neurons. For a perceptron a simple step-like function is used as the activation function of the central computing neuron.
Remark: In the literature you will find perceptron or Adaline architectures with a central layer that contains multiple computing neurons. In such cases all input neurons are connected to all of the central compute neurons. We will not consider such a configuration in this post series.
Weights
The w1 and w2 characterize connections from the input neurons to our central neuron CN. w1 and w2 are adaptable parameters of our simple network. In general an ANN-parameter which controls the amplitude modification of a signal when it is transported along a connection and received by a target neuron is called a weight.
Weights determine how much of an output signal produced by a sender neuron is used on the input side of a receiver neuron. I, therefore, regard a weight as a property of the receiving neuron for an incoming connection from a particular sender neuron.
Note that the CN neuron does not work on the incoming signals separately. Instead Z is created as a linear superposition. Linear because the coefficients w1 and w2 are regarded as constants (at least during a processing step).
Note: We will have to find optimal values for the weight parameters to enable an ANN to solve a certain type of task properly. The process during which we determine optimal weight values is called training of the ANN (see below).
Remark: There are classes of networks for which it is reasonable to associate weights with the sender neurons. I will not consider such cases here.
Input features and input feature space
Input data fed into an ANN represent real or abstract objects. Objects have properties. An ANN works on digitized object data. This in turn requires that an object’s properties must be quantifiable. I.e.: We describe objects by assigning numerical values to at least one, but in general to an appropriate set of many quantifiable properties. An object property is often called a feature in ML contexts.
We use letters \(\operatorname{K}_1, \operatorname{K}_2, … \) to symbolize such features of our input data. To enable computations with object features they are e.g. described by floating point numbers or discrete integer numbers. (In some special cases even complex numbers may appear). Mathematically we represent a feature \(\operatorname{K}_n \) by a corresponding variable \(k_n\) which can take a specific value \(k_n^s\) for a specific object \( \pmb{O}_s \).
Thus, an object \( \pmb{O}_s \) is described by a tuple of concrete number values for variables \(k_1, \, k_2, \, …\, k_n \).
All the features \(\operatorname{K}_n, \, …\, \operatorname{K}_n \) can together be represented by a n-dimensional coordinate system with orthogonal axes (Euclidean coordinate system [ECS]). A particular ECS-axis reflects the range of values a related specific feature variable can take. We call the mathematical space spanned by the ECS the (representational) “feature space” of the objects we work with.
A specific object \( \pmb{O}_s \) corresponds to a single point in such an ECS. The coordinates of this point are given by the tuple \( (k_1^s, \, k_2^s, …\, k_n^s) \). The points corresponding to a set of given objects fill the space in form of some (discontinuous) distribution. The points may e.g. form distinguishable clusters in the feature space.
Note: The data for any distinct input feature which we want to feed into an ANN must be received by a dedicated input neuron. I.e.: networks operating on data of objects with n features require n input neurons. Input neurons may be arranged in a so called input layer of the ANN. The values \(\left(k_1^s, \,k_2^s\right)\) of each object \( \pmb{O}_s \) must be presented to the input neurons IN_1 and IN_2 at the same time.
In this post series we will work with a 2-dimensional feature space, only. Our neuron will operate on objects which are represented by just two features \(\operatorname{K}_1\) and \( \operatorname{K}_2 \). Regarding the input channels \( \operatorname{K1} \) and \( \operatorname{K2} \) of our simple perceptron the “signals” arriving there reflect nothing else then the quantified values \(\left(k\,_1, \, k_2\,\right) \) of the two object features. So, \( \operatorname{K1} \), \( \operatorname{K2} \) are almost interchangeable with \(\operatorname{K}_1\), \(\operatorname{K}_2 \). But note that we may have to perform some scaling of feature values before we transfer the resulting values as signal strengths to the input neurons.
How big can a feature space dimension become? For real world ML-examples the feature space may have many more dimensions, up to some millions. I.e. the objects a ML-algorithm has to work with may be characterized by very many features. Example are high-resolution images for which each pixel defines a feature.
Position vectors: For those who are familiar with vectors: \( k_1^s \) and \( k_2^s \) can be regarded as component values of a position vector \(\left(k_1^s, \,k_2^s\right)^T\) (with “T” symbolizing the transposition operation; I normally write vectors in vertical direction).
Remark on notation: In this series I use big letters to symbolize logical object features (properties), signal channels or logical signal data at certain locations in a network. Small letters symbolize respective mathematical variables, which can take specific values for a signal at a particular location within or at the borders of the ANN. I sometimes write formulas also for big letter quantities when I want to indicate that the relations hold for the processed data of all objects (of a defined object set).
Distinct processing steps / Batches of objects
Defined values of signals occur at distinct sequential processing steps of the network along an assumed processing timeline. There is a well-defined order of process execution while a signal propagates through a network and its (sequential) layers. I.e. our network has a kind of logical heart-beat: At each beat all layers and neurons perform a certain operation leading to new, well defined variable values for signal amplitudes at all locations within and at the borders of the network.
Remark on batch processing: Objects may be presented to a neural network in sets \( \left\{\, \pmb{O}_{s1},\, \pmb{O}_{s2}, \,…\, \pmb{O}_{sm} \, \right\} \). Such a set of objects ( = tuples) could in numeric simulations correspond to a batch. Whether object data of a batch are processed by a CPU or GPU in parallel (i.e. as a unity) or sequentially is a question of the numerical algorithms representing the ANN and the CPU/GPU’s architecture.
Fictitious example objects
In our case the neuron shall deal with objects having exactly two features \( \operatorname{K}_1 \), \( \operatorname{K}_2 \). They are mathematically represented by variables k1 and k2. Let us take the following fictitious example:
We have a substance, a potential allergen, to which a certain group of people, GA, reacts very allergic. Members of another un-allergic group, GU, only react slightly to a certain dose of the allergen. We measure the amount of allergen people are exposed to by a variable k1. So, the first feature of our objects is the level of allergen exposition. The allergic reaction itself may instead be measured by the level of something like the histamine concentration in the blood. This gives us a second variable k2. So, the second feature is the level of allergic reaction.
Our basic objects, therefore, are allergy tests done with various people. An object therefore does not necessarily correspond a person, yet. First of all, the tests would fall into two distinguished groups – not necessarily the tested persons. To overcome this distinction a bit let us further assume that there is a theory proclaiming a linear correlation between k1 and k2 for investigated groups of persons:
In our example we call \(\alpha_G\) a “reaction coefficient”. According to the assumed theory \(\alpha_G\) must have a big value for persons of group GA and a small value for members of group GU. Let us further assume that we have some measured data for both groups, which we plot in a 2-dimensional diagram. Data points are given by pairs of concrete data values \( (k_1^s, k_2^s) \) submitted to the input channels K1 and K2, respectively:
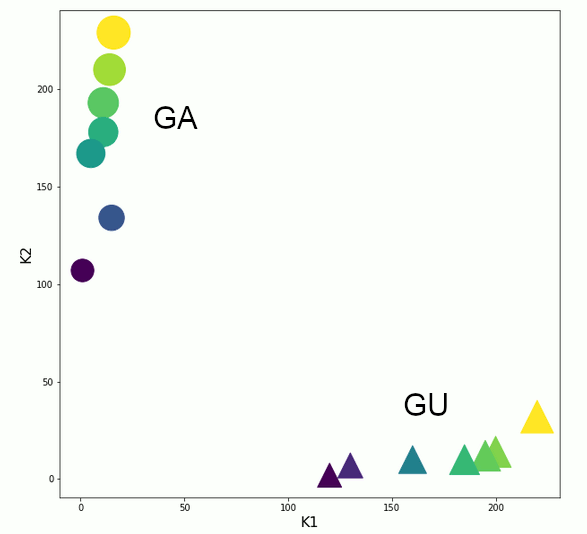
An “object” in our case thus is a test of an exposed person. The object is characterized by a pair of concrete values \( (k_1^s, k_2^s) \). Each object corresponds to a point in our diagram. K1 and K2 define the axes of an (Euclidean) coordinate system for our data points. The axes K1 and K2 span our 2-dimensional “feature space“. The data for the groups GA and GU obviously form two distinct data clusters in the feature space.
Our few measured object data obviously do not fulfill our assumption of a linear relation between K1 and K2 in ideal way, but only approximately. However, we could lay a straight line from the origin of our coordinate system through each of our two point clusters (see below). We will later calculate such straight lines by a method called “linear regression”. An individual data pair will deviate somewhat from the averaging straight line of its group.
Data distribution in the feature space
Obviously, our two clusters only fill distinct regions of the feature space. A reason for this might be that we have not investigated enough objects, yet. We can and will not exclude that further measurements will show other groups of people with different reaction coefficients than GA and GU. GA and GA would then just mark the most extreme groups of objects. But, well, for the time being the displayed few data points is all we have.
Our given data also reveal an empty region near the origin of the coordinate system. For GA the data could indicate that even for a small allergen concentration the reaction is always above some minimum level. For GU the reaction may have not been measurable below a certain threshold value.
For real world examples we would need to find out why the data may not fill certain areas of the data space. Especially under circumstances where some theory claims that we should find data in such regions, too. This may impact the way of how we train our ANN.
Two proper tasks for our neuron – binary or multiclass classifier
Let us define two tasks which our simple ANN shall eventually solve:
- Task 1: Whenever we present new data pairs (k1, k2) to the network it shall tell us whether the object corrrsponds to an allergic reaction or not. I.e., the network shall answer the question: Does the object belong to group GA or to group GU? The expected output of our neuron is a prediction concerning the group membership of an object.
- Task 2: If we later wanted to differentiate more than 2 groups our ANN should be able to identify a proper group for any input data. The solution for a proper output creation should be based on our theory.
Task 1 is a typical classification task: The ANN gets input data of an unknown object and must determine to which of a number of defined groups the object belongs. As long as we consider only two groups we want our ANN to become a so called binary classifier. But task2 will force us to find a way to extend it to a multiclass classifier.
Supervised training
To be able to solve such tasks the neuron must be trained. A so called supervised training is a phase during which a ANN is confronted with a set of object data for which the solution of the task is already known. In the case of a classification task we deal with training objects for which the membership to a group has already been well defined.
During a “supervised training” we give the network a feedback regarding the deviation of its predictions (i.e. its produced output) from a value representing the known truth. This requires that also a prediction must be expressed in form of (discrete) number values. We will later see how to get such prediction values from the output of our neuron.
Remark: There exist other forms of training for other types of ANNs, e.g. un-supervised or self-supervised trainings. We will focus on supervised training in this post series, only.
Decision criteria for classifications
In the case of a classification we need some criteria which the output data of an ANN must fulfill to make a prediction with respect to the group membership of an object clear and unambiguous.
Given the clusters of our data in the feature space we may come to the conclusion that we have multiple options to define whether a new data point (of some new object) belongs to either group GA or group GU – or to no defined group. The following sketch supports this idea:
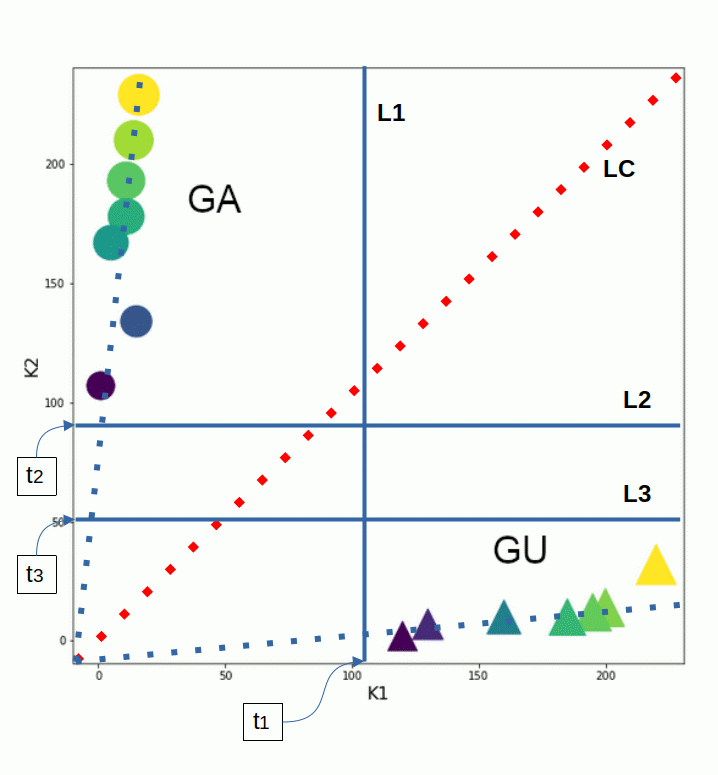
I have included one vertical separation line L1 and two horizontal separation lines L2 and L3. The respective threshold values on the axes are t1 and t2, t3. Whenever \(k_1^s\) and \(k_2^s\) of a given object fulfill relations relative to the respective threshold values marked by the lines we could assign them to a group. A first very simple condition could be
Or we could define criteria with respect to boxes defined by L1 and L2 or by L1 and L3. Note, however, that all these approaches would correspond to new theories or models for the relation between K1 and K2.
With respect to the diagonal, red dotted line we could also define that an object represented by (k1, k2) is a member of GA or GU if it is located to the left or right of the diagonal line, respectively.
Now, we got some ideas of what our ANN may need to “learn” by a training to later perform a reliable binary classification of our given objects.
BUT: The criteria given above would not be useful for a training process. Actually, we would not need any ANN at all as the criteria were given with respect to the input data and not with respect to any output the computing neuron will produce. It is however the trained ANN’s output which must support the requested decision.
Furthermore, even the simple criteria discussed above are too specific with respect to data points for yet unknown objects. In addition new data points may render our assumed linear theory wrong and show more complex clusters. At the moment we have, however, no idea what kind of complexity regarding the data distribution our network could handle after a proper training.
Note: Criteria for classification must be defined with respect to the output data an ANN produces. Clusters and respective separation lines in the original feature space only give first hints of how a reasonable separation of groups or clusters could or should look like.
Our situation is actually somewhat opposite:
During and after training the predictions regarding group membership will depend on the ANN’s output and some decision criteria we impose on it. We can then re-translate the ANN’s decisions into separation lines in the objects’ feature space. The separation lines which a trained ANN (with a non-linear activation function) produces in a 2-dimensional feature space due to output related decision criteria may be curved and complex. For a given and trained ANN such lines should be plotted and evaluated with respect to their usability and consistency with proclaimed theories.
Remark: In multidimensional feature spaces object clusters may be separated by complex curved multidimensional surfaces – so called hyper-surfaces.
The important points to remember are the following:
- Defining proper classification criteria may depend on the available data, the complexity of their arrangement in the feature space (which we may only know to a certain extend) and on assumed theories about data relations (which may be incomplete and even wrong).
- Classification criteria may also depend on the capabilities of a given ANN. In our case we need to analyze in what way the neuron’s output depends on the input data and the weight parameters w1 and w2. If the activation function f(Z) is a non-linear function we may have to take into account features of f().
Output data and their dependency on ANN-parameters and the input
Our simple ANN has only one (!) output channel. Still we must use this output to distinguish at least two apparent groups of objects. This may on first sight appear as a contradiction. But it is not. However, it requires certain properties of the function f(Z) to allow for for clear distinctions and decisions.
Our sketches imply that even the output A of our single neuron is a relatively complex function of the input data. We name the variable for the strength of the output signal “a” and conclude that it actually is a function a():
Instead of defining classification criteria with respect to \((k_1, \,k_2)\) we need to define reasonable criteria which \( a(k_1, k_2) \) must fulfill. \( a(k_1, \, k_2) \) obviously depends on two variables. It is a 2-dimensional function, which for a defined input tuple \((k_1, \,k_2)\) and given parameters w1, w2 produces one real value. Before we can reasonably define classification criteria we must better understand how \( a(k_1, k_2) \) behaves for certain types of activation functions f(Z).
The original version of a perceptron (published by Frank Rosenblatt, 1957) used a simple step-function (a so called Heaviside function) as activation function for a binary classifier. This makes a description of the gradient descent method very easy. However, I will take the freedom to deviate from this original approach. We will instead use a continuous non-linear function, the so called sigmoid function (see the next posts). Historically and formally, this freedom corresponds to steps from a plain perceptron over a variant with a linear activation function to something called a logistic regression modeller or classifier.
Complexity: For general ANNs of many layers, each with many neurons and millions of connection related weight parameters as well as different functions f(), the dependency of outputs \(a_1(), \, a_2(), … \) on inputs and network parameters may become so complex that we may not be able to explain the networks behavior in a precise manner. We then would need clever and simplifying, but qualitatively correct analytical methods to understand how an ANN reacts to certain input data.
In our case we will be able to handle everything analytically as we deal with an extremely simple network, simple data and because we will choose a relatively simple activation function f().
Conclusion
Enough for today. In this post we have defined a very simple artificial neural network with two input neurons and a single computing neuron that produces some output via an activation function. We had a look at the way objects are represented by numerical (real or integer valued) data and how these data are fed into our ANN via input channels. For a fictitious example we saw a clustering of the available input data in the two-dimensional feature space. But we have no clue, yet, how we could use the output which our compute neuron will produce for such input data to solve a binary or multiclass classification task.
In the next post of this series we will have a look at three types of functions f(Z) which can help us with our classification problem.